- Le choix de l'instrument pour imager en planétaire doit porter en
premier lieu sur sa capacité à produire de bonnes images, en particulier au centre de l'image. Les planètes étant peu étendues sur le champ de l'image, le maximum de qualité et de résolution seront recherchés dans cette zone centrale de l'image.
Cette qualité dépend des matériaux utilisés (type de verre par exemple, traitement de surface, etc), du type de formule optique utilisée (lunette,
télescope) et de leur mise en œuvre (qualité de polissage des surfaces optiques, alignement de celles-ci, etc.
Pour imager en ciel profond, c'est la luminosité de l'instrument qui prime. La qualité de l'instrument n'est pas aussi primordiale qu'en planétaire.
D'autres paramètres de choix interviennent également, plus personnels : le coût, la transportabilité, l'envie, la maîtrise de la qualité sur toute la chaîne, les réglages et entretiens nécessaires, etc...
- La qualité de fabrication
-
C'est ce qui coûte le plus cher et qui oppose la qualité industrielle à celle de l'artisan. Elle va généralement de paire avec
la qualité des matériaux utilisés (type de verre, pièces mécaniques d'assemblage et de réglage, revêtement anti-reflet, etc).
Sur le plan optique, la qualité d'un instrument s'évalue par sa capacité à faire converger les rayons lumineux partis d'un même point éloigné dans l'espace (en fait des fronts d'ondes, "des ronds dans l'eau" lumineux) en un point focal (qui appartient à l'image que l'instrument "fabrique"), et sans les "déformer".
Ce cheminement dans l'instrument des rayons lumineux (et donc des fronts d'onde) obéit aux lois de l'optique, qui sont, pour une grande part, purement géométriques.
Des surfaces théoriques de verre sont calculées pour faire dévier les rayons conformément à ces lois géométriques, et les faire converger sur le plan focal. Ces surfaces sont de natures diverses : planes, sphériques, paraboliques, hyperboliques... voire plus "tordues" encore... et peuvent être transparentes (lentilles) ou réfléchissantes (miroirs).
Toute la difficulté tient alors dans la réalisation des-dites surfaces en polissant minutieusement un matériaux, généralement du verre, en respectant le mieux possible la forme générale de la surface théorique (qualité de forme) et en rendant le plus lisse possible le résultat du polissage (qualité de surface).
La qualité de forme s'apprécie globalement par rapport à l'écart maximum à la forme théorique idéale ( écrt P-V : peak to valley, crête à crête en français) et se mesure en unité de longueur d'onde (généralement celle de la lumière jaune notée L, prononcer "lambda"). Une bonne optique montre une erreur de L/4. Les très bonnes font mieux que L/10 (soit 0,05 µm).
La qualité de surface s'apprécie par un paramètre "statistique" permettant de se faire une idée de la rugosité de la surface optique (qualité du polissage) : une sorte d'écart moyen à la surface moyenne théorique (Root Mean Square, noté RMS). Cette rugosité va nuire au contraste de l'image : plus elle sera élevée, plus l'image sera diffuse, "brumeuse" et donc moins en mesure de permettre à l'observateur de discerner des détails faiblement contrastés (ce qui peut diminuer le pouvoir de résolution de l'instrument). Le RMS d'une optique moyenne se situe autour de L/20.
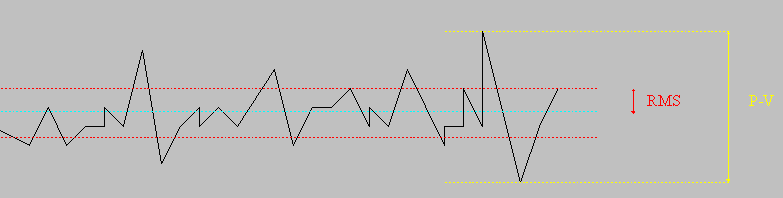
Rugosité du polissage
- La formule optique
- Indépendamment du talent du fabricant, il existe un très grand nombre de
combinaisons optiques permettant de produire une image d'une scè réelle. Depuis Galillée puis Newton, ces "formules" optiques reposent sur le principe de la lunette (avec des
lentilles) ou sur celui du télescope (avec des mirroirs).

Lunette de Galilée et le télescope de Newton
L'avantage des lunettes repose sur une moindre sensibilité aux défauts de surface : un défaut local d'épaisseur d produira une variation d'environ d/2 du chemin optique parcouru par le front d'onde pour la lentille, et de 2d pour le miroir. L'impact de la qualité de polissage sera donc quatre fois plus important sur la qualité d'image fournie par le miroir que sur celle de la lentille.
En revanche, l'inconvénient majeur des lentilles est qu'elles se comportent localement comme un prisme et donc, décomposent la lumière : elles ont tendance è iriser les images, è montrer un défaut de chromatisme. A l'inverse un miroir réfléchit toujours la lumière de la même façon, indépendamment de sa longueur d'onde. Il ne présente aucun défaut de chromatisme.
A partir d'une certaine taille, il devient en outre très coûteux et lourd de fabriquer une lentille (il ne doit pas y avoir de bulle à l'intérieur !). De plus, son épaisseur diminue fortement sa transparence alors que ses bords minces ne permettent plus de soutenir son propre poids. Pour le même diamètre, le miroir peut rester assez mince et plus léger sans diminuer ses performances, bien au contraire.
- Les principales caractéristiques
- Quelle que soit la formule optique choisie, trois caractéristiques essentielles de l'instrument optique demeurent :
- sa capacité à produire une image plus ou moins grande : son grandissement ;
- sa capacité à produire une image détaillée, nette et contrastée : son pouvoir de résolution ;
- sa capacité à produire des images les plus lumineuses possibles.
Le grandissement offert par l'instrument est proportionnel à sa longueur focale F ( en gros la longueur de la lunette qui lui est équivalente) alors que sa résolution est, de façon approchée, inversement proportionnelle au diamètre de l'ouverture de l'instrument par laquelle la lumière arrive (diamètre de l'objectif D) :
résolution = 120/D
(résolution exprimée en seconde d'angle, soit 1/3600°, diamètre exprimé en mm) Pour se faire une idée, , une seconde d'angle correspond à un écartement de 1 mm vu à une distance de 200 mètres.
Enfin, il est également utile sur le plan pratique d'évaluer la luminosité des images produites : elle est proportionnelle à la surface collectrice de lumière (donc proportionnelle à D²) et inversement proportionnelle à la surface de l'image sur laquelle cette lumière collectée s'étale : 1/F².
On utilise généralement le rapport F/D pour caractériser cette luminosité de l'instrument. Pour un diamètre double (2D) et une focale double (2F) la luminosité sera ainsi la même (2F/2D = F/D) car il y aura 4 fois plus de lumière collectée (4D²) qui s'étalera sur une image aux dimensions (largeur x hauteur) deux fois plus grandes puisque proportionnelles à la focale, et dont la surface sera quatre fois plus grande (4F²).
Ce qu'il faut retenir pour imager en planétaire : les planètes sont d'apparence très petites, de l'ordre d'un centième de degré d'angle apparent. Il faut donc grandir beaucoup et utiliser la plus grande focale possible (entre 5 et 10 mètres de focale). Pour discerner des détails à la surface d'une planète, il faut un pouvoir de résolution très élevé, se mesurant en dix-millièmes de degré. Il faudra donc privilégier des instruments aux diamètres le plus grand possible, avec des focales les plus longues possibles...
Ce qu'il faut retenir pour imager en ciel profond : il faut un instrument le plus lumineux possible, donc avec un rapport F/D le plus petit possible. Un diamètre plus grand, permettra de déceler de plus faibles étoiles.
- Les limitations physiques
-
Mais l'histoire n'est pas si simple... ni seulement géométrique...
Une lunette ou un télescope de Newton sont les formules les plus simples. Mais avec un objectif de 30cm de diamètre et de six mètres de focale, les difficultés arrivent : coût pour la lunette, contraintes mécaniques, encombrement et poids.
Ces deux formules sont excellentes proches de l'axe optique et conviennent parfaitement en imagerie et observation planétaire.
En revanche, en imagerie du ciel profond, le rapport F/D est généralement bien adapté, mais l'imagerie du ciel profond exige des champs image beaucoup plus larges qu'en planétaire et sans déformation sur les bords (coma, chromatisme ect).
Des correcteurs doivent être ajoutés, et la formule devient complexe et plus couteuse.
Les opticiens et les constructeurs se sont donc ingénié à trouver des formules optiques plus compactes et donc plus pratiques à utiliser et moins chères à produire que les lunettes.Le principe est simple : on intercale entre l'objectif et l'image un dispositif qui agrandit l'image "avant" qu'elle ne se forme : en utilisant soit une lentille (de Barlow par exemple) pour les lunettes et les télescopes de Newton, soit un miroir secondaire grandissant (à l'instar des multiples formules de type Cassegrain, du nom d'un inventeur français contemporain de Newton).
On apporte évidemment quelques défauts supplémentaires sur le chemin optique mais on gagne énormément (un facteur 5 à 10) en encombrement longitudinal comparativement à une lunette.
Pour les formules de type Cassegrain, le miroir secondaire (sphérique, parabolique voire hyperbolique ) tend à occuper une surface assez importante qui n'est plus aussi négligeable que pour la formule Newton (secondaire plan proche du foyer). De plus les axes optiques des différents éléments doivent être rigoureusement alignés ("collimatés"). Dans le cas contraire, les performances des meilleurs instruments s'éffondrent au moindre déréglage, ce qui est rarement le cas pour une lunette réputée indéréglable.
Les perturbations sont introduites par la présence du miroir secondaire qui bloque le passage des rayons lumineux en direction du miroir primaire (causant une obstruction notée o et exprimée en fraction du diamètre d'ouverture). Ces perturbations ont été modélisées pour montrer que l'obstruction a tendance à diminuer le diamètre efficace de l'instrument :
Deff = D x (1-o²)² x e-(2πRMS)²
et s'ajoutent à celles dûes à la qualité du miroir principal (RMS), ou à la qualité intrinsèque des matériaux utilisés (transparence du verre, réflectivité du miroir, etc).
Ces formules ont été intégrées dans le tableau qui suit et permettent de comparer, sur des images moyennement contrastées, des performances théoriques des instruments que j'utilise à celles d'un instrument parfait... on ne peut plus théorique...
L'ETX90 est ainsi nettement moins bon que l'ED80, elle-même très éloignée des performances du Maksutov M715.
http://www.astrophoto.fr/
http://astrosurf.com/luxorion/menu-technique.htm
http://www.astrosurf.com/texereau/
